Sample Size Calculation with GPower
in-house workshop
Wilfried @ SQUARE
square.research.vub.be
April 02, 2023
Sample Size Calculation with GPower
Goal
- to introduce key ideas
- to offer a perspective for reasoning
- to offer first practical experience
Target audience
- primarily the research community at VUB / UZ Brussel
Feedback
- help us improve this document
wilfried.cools@vub.be
- help us improve this document
1 + 1:30 introduce researchers to key ideas (know how), to help you reason about it (why), and make sure you are able to (get it done)
Program
Part I: understand the reasoning
- introduce building blocks
- implement on t-test
Part II: explore more complex situations
- beyond the t-test
- simple but common
GPower
- not one formula for all
- a few exercises
1:30
first focus on essence with simple example then extend and exercise
Sample size calculation: demarcation
How many observations will be sufficient ?
- avoid too many, because typically observations imply a cost
- money / time → limited resources
- risk / harm → ethical constraints
- depends on the aim of the study
- research aim → statistical inference
- research aim → statistical inference
- avoid too many, because typically observations imply a cost
Linked to statistical inference (using standard error)
- testing → power [probability to detect effect]
- estimation → accuracy [size of confidence interval]
5:00 if going slow
It is about answering your research question while avoiding avoidable costs, only works when focused on inference because of the standard error
Sample size calculation: a difficult design issue
Before data collection, during design of study
- requires understanding: what is a relevant outcome ?!
- requires understanding: future data, analysis, inference (effect size, focus, ...)
- decision based on (highly) incomplete information, based on (strong) assumptions
Not always possible nor meaningful !
- easier for confirmatory studies, much less for exploratory studies
- easier for experiments (control), less for observational studies
- not possible for predictive models, because no standard error
- NO retrospective power analyses → OK for future study only
Hoenig, J., & Heisey, D. (2001). The Abuse of Power:
The Pervasive Fallacy of Power Calculations for Data Analysis. The American Statistician, 55, 19–24.
Alternative justifications often more realistic:
- common practice, feasibility, ... or a change of research aim (description, pilot, ...)
- less strong, puts more weight on non-statistical justification (importance, low cost, ...)
8:00
What do you want !?!! because about how to ensure you get it ! And what will the data look like, in practice, not easy because unknown, voodoo Maybe not always so important because maybe often it is not possible nor meaningful Then focus on what you can do... explain, convince Show you have given it careful thought
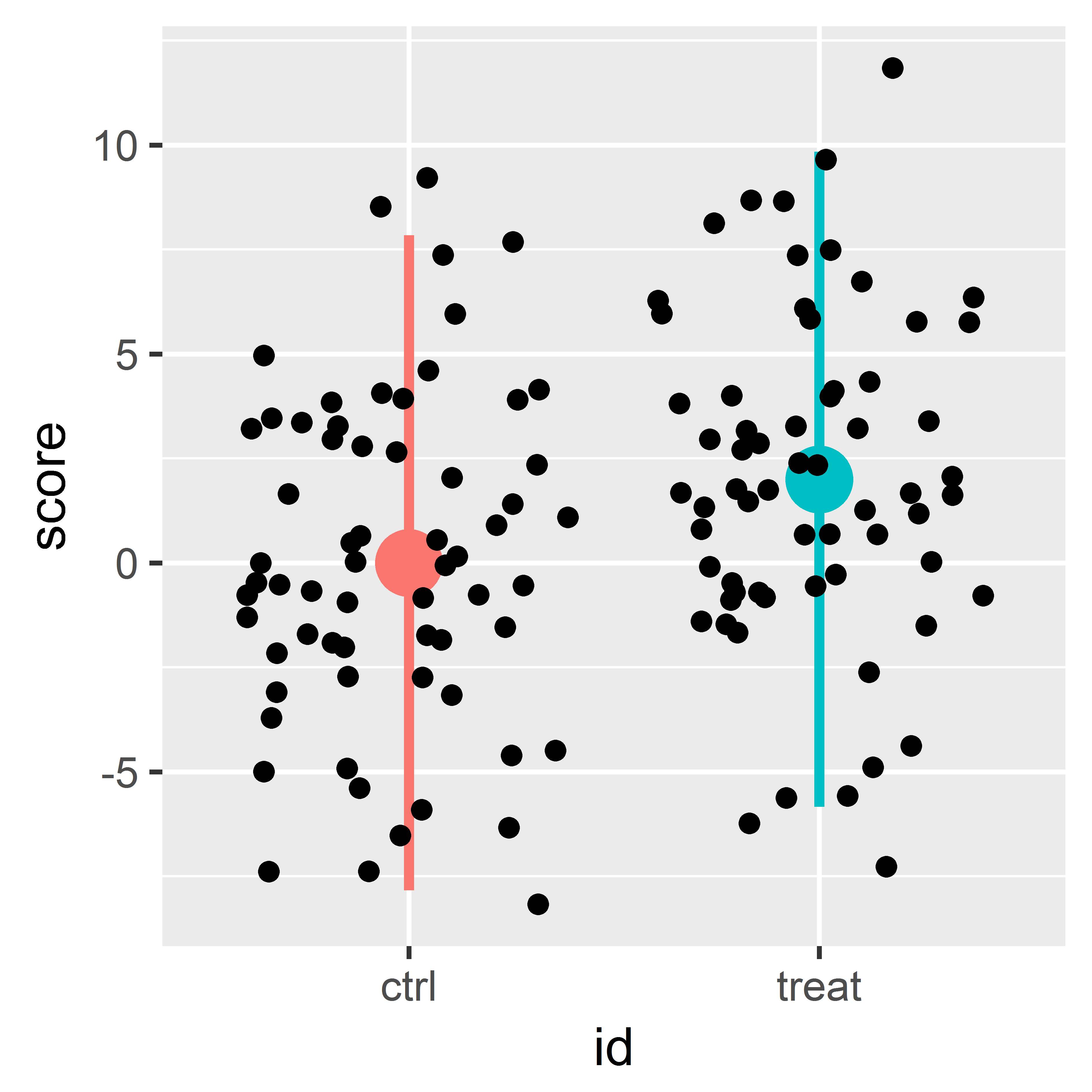
Simple example confirmatory experiment
Example: does this method work for reducing tumor size ?
evaluation of radiotherapy to reduce a tumor in mice
comparing treatment group with control (=conditions)
- tumor induced, random assignment treatment or control (equal if no effect)
- after 20 days, measurement of tumor size (=observations)
- happy if 20% more reduction in treatment !! (=minimal clinically relevant difference)
intended analysis: unpaired t-test to compare averages for treatment and control
SAMPLE SIZE CALCULATION:
- IF average tumor size for treatment at least 20% less than control (4 vs. 5 mm)
- THEN how many observations sufficient to detect that difference (significance) ?
2:00
Just a first possible example where all is straightforward. It considers the goal, the statistical test.
Reference example
- Reference example used throughout the workshop !!
Apriori specifications
- intend to perform a statistical test
- comparing 2 equally sized groups
- to detect difference of at least 2
- assuming an uncertainty of 4 SD on each mean
- which results in an effect size of .5
- evaluated on a Student t-distribution
- allowing for a type I error prob. of .05 (α)
- allowing for a type II error prob. of .2 (β)
Sample size
conditional on specifications being true
2:40
Another example, with values used throughout the workshop. WRITE delta 2 sigma 4 so effect size .5 alpha .05 beta .2 thus power .8 n ?
Formula you could use
For this particular case:
- sample size (n →
?) - difference ( Δ =signal →
2) - uncertainty ( σ =noise →
4) - type I errors ( α →
.05, so Zα/2 → -1.96) - type II errors ( β →
.2, so Zβ → -0.84)
- sample size (n →
Sample size = 2 groups x 63 observations = 126
Note: formula's are test and statistic specific
logic remains sameThis and other formula's implemented in various tools
our focus:GPower
n=(Zα/2+Zβ)2∗2∗σ2Δ2
n=(−1.96−0.84)2∗2∗4222=62.79
2:00
It is simple to extract the sample size using only these numbers. The alpha and beta is interpreted on a normal distribution, as cut-off values for probabilities by quantiles. This is the simplest case, not the t-distribution which depends on the degrees of freedom.
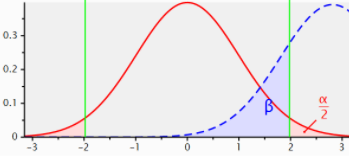
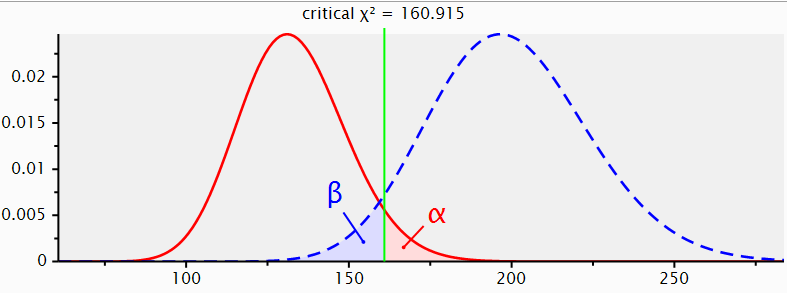
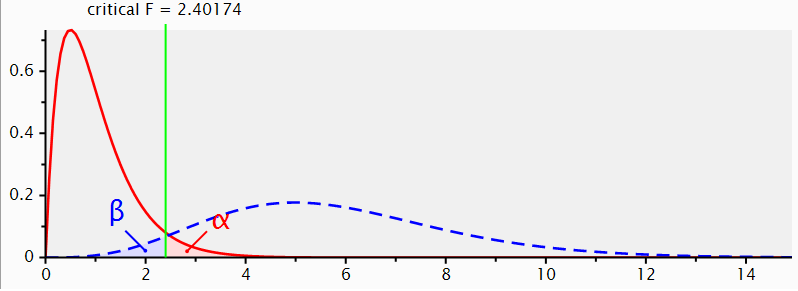
GPower: the building blocks in action
4 components and 2 distributions
- distributions: Ho & Ha ~ test dependent shape
- SIZES: effect size & sample size ~ shift Ha
- ERRORS :
- Type I error ( α ) defined on distribution Ho
- Type II error ( β ) evaluated on distribution Ha
Calculate sample size based on effect size, and type I / II error
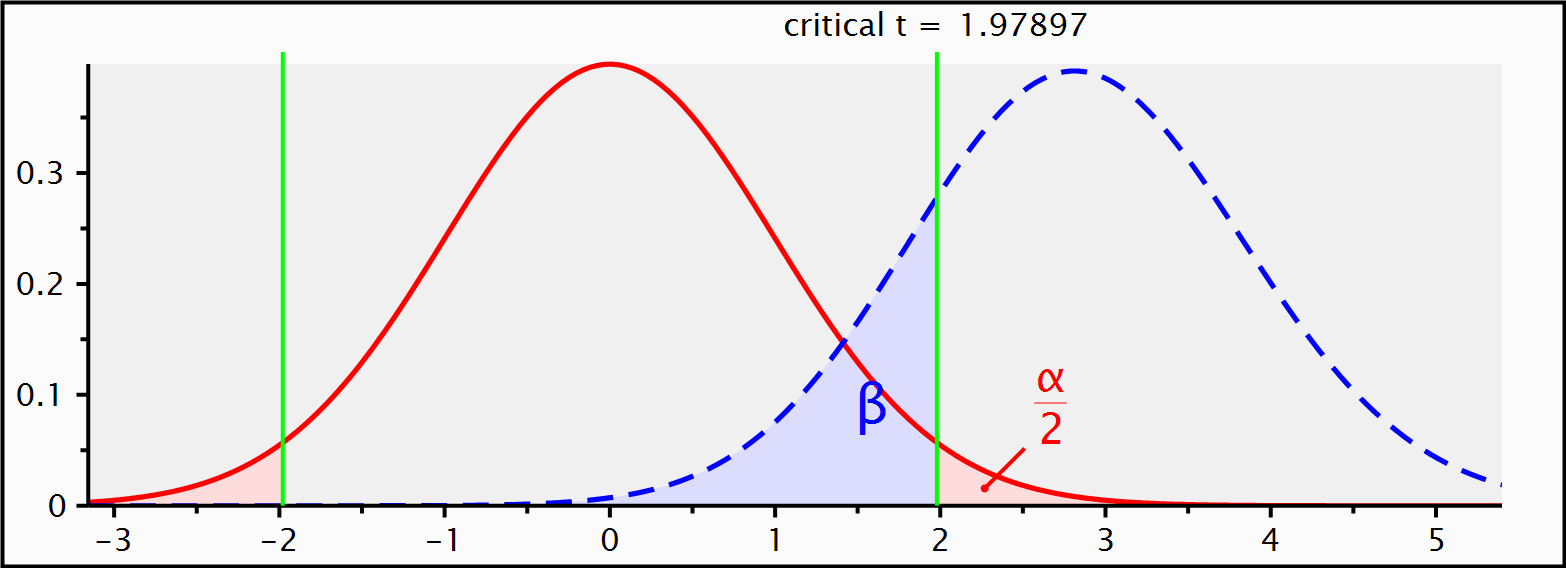

2:00
One of the distributions reflects the absence of effect, the other combines the size of the effect and the information available to try and detect that effect. The actual distributions depend on the statistical test of interest. The shift depends on both; effect size and sample size. The shift has consequences for how much of the Ha distribution is beyond the cut-off at Ho distribution. The only issue is how far the distribution shifts...
GPower: a useful tool
Use it
- implements wide variety of tests
- free @ http://www.gpower.hhu.de/
- popular and well established
- implements various visualizations
- documented fairly well
Maybe not use it
- not all tests are included !
- not without flaws !
- other tools exist (some paying)
- for complex models: impossible
alternative: simulation (generate and analyze)
2:30
GPower because it offers calculations for different tests, no need to study formulas. There are good reasons to use it, but... not all is perfect.
GPower statistical tests
- Test family - statistical tests [in window]
- Exact Tests (8)
- t-tests (11) →
reference - z-tests (2)
- χ2-tests (7)
- F-tests (16)
- Focus on the density functions
- Tests [in menu]
- correlation & regression (15)
- means (19) →
reference - proportions (8)
- variances (2)
- Focus on the type of parameters
1:30
Before focus on one of the 11 t-test, or one of the 19 means comparisons, however you want to look at it. Various other tests exist, categorized in one of two ways.
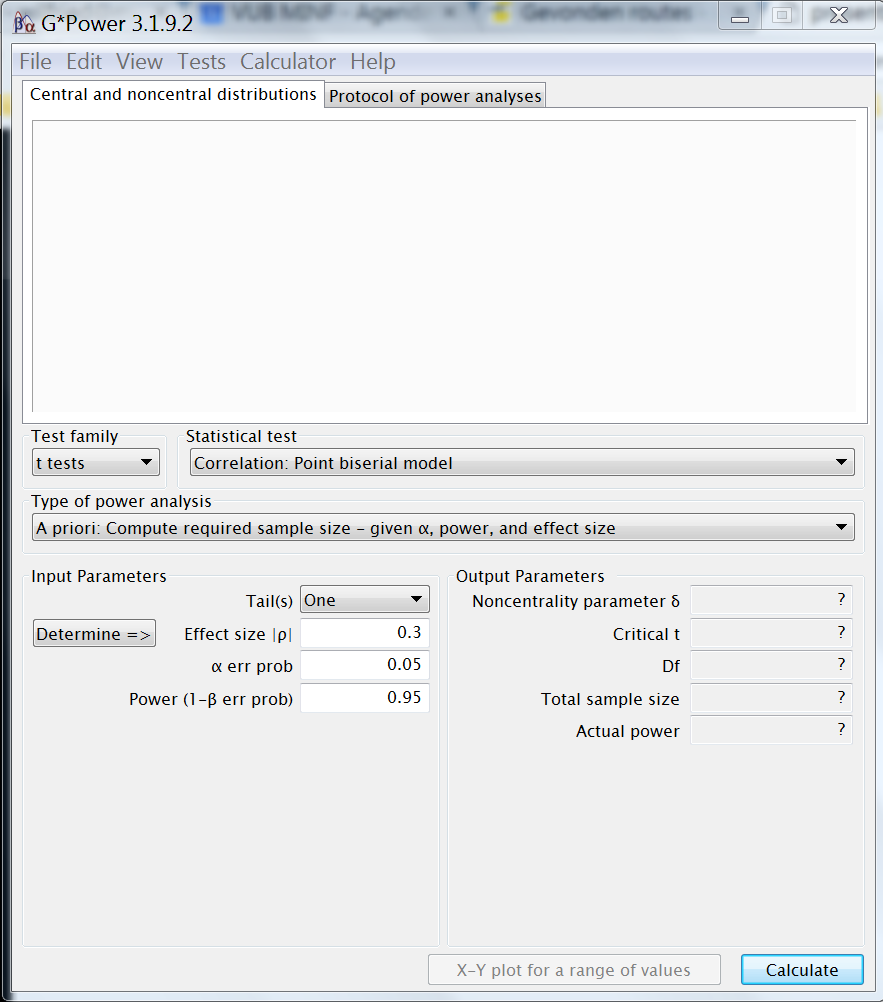
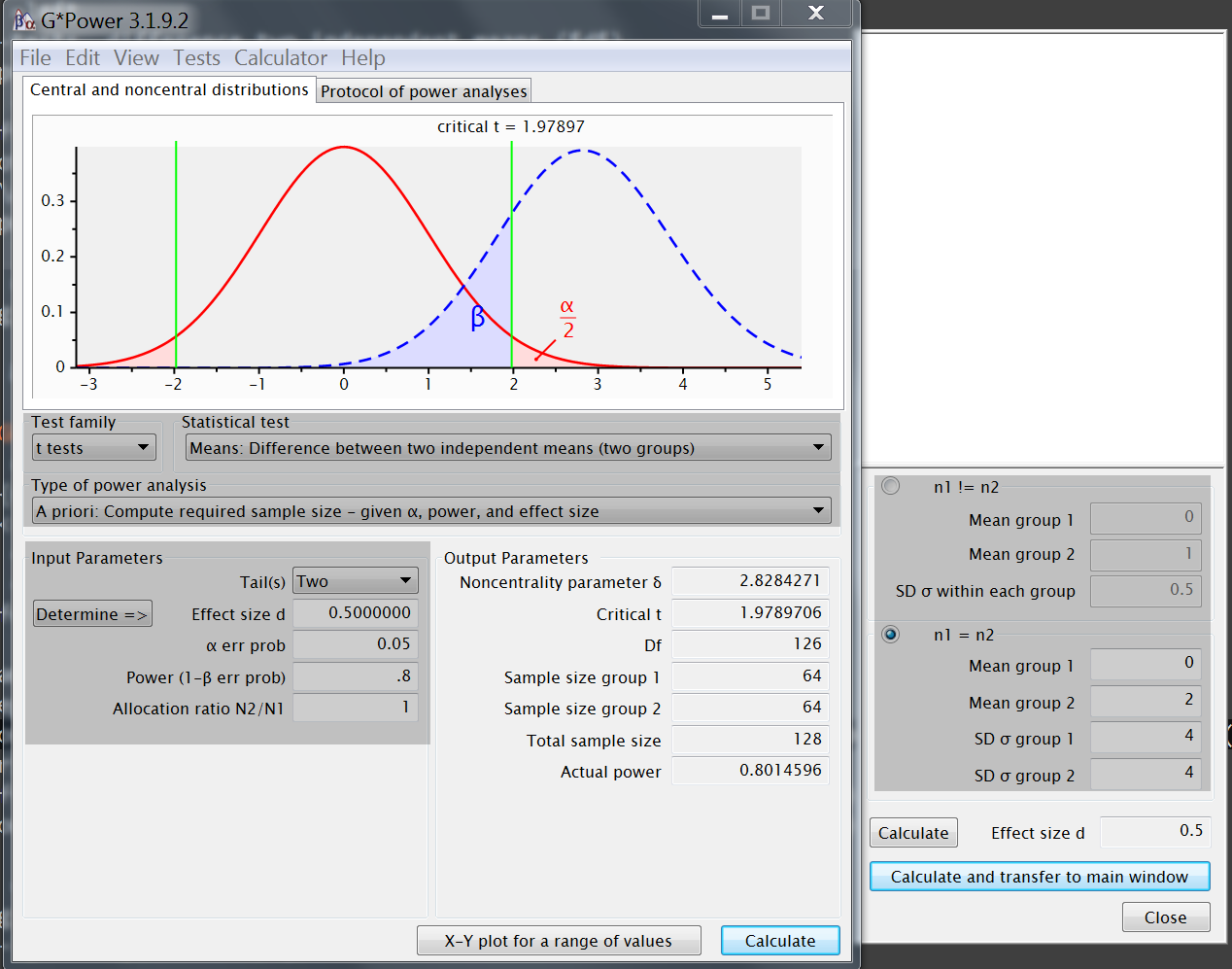
GPower input
~ reference example input- t-test : difference two indep. means
- apriori: calculate sample size
- effect size = standardized difference
- Cohen's d
- Determine =>
- d = |difference| / SD_pooled
- d = |
0-2| /4=.5
- α =
.05
2 - tailed( α /2 → .025 & .975 ) - power=1−β =
.8 - allocation ratio N2/N1 =
1
(equally sized groups)
2:00
For the reference example the input is given, t effect sizes are specified with 'determine'.
We choose a test, type, to get sample size, we use effect size 2/4, alpha .05 and beta .2.
SHOW MARKER
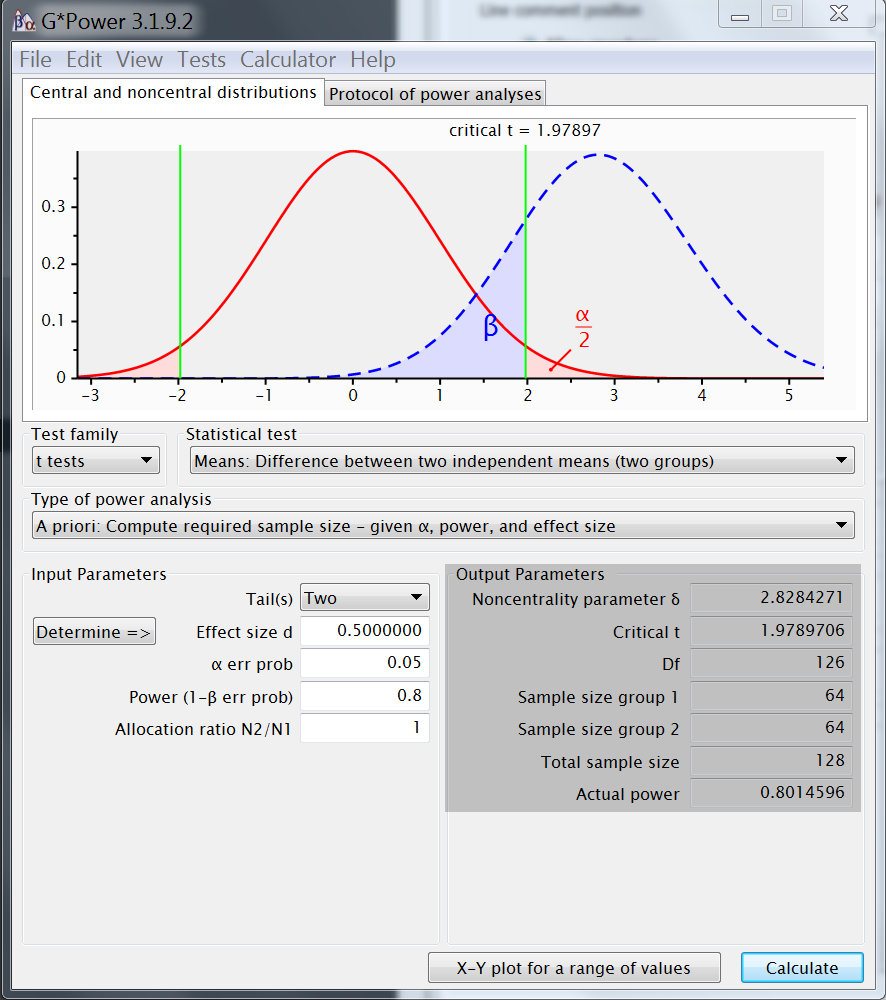
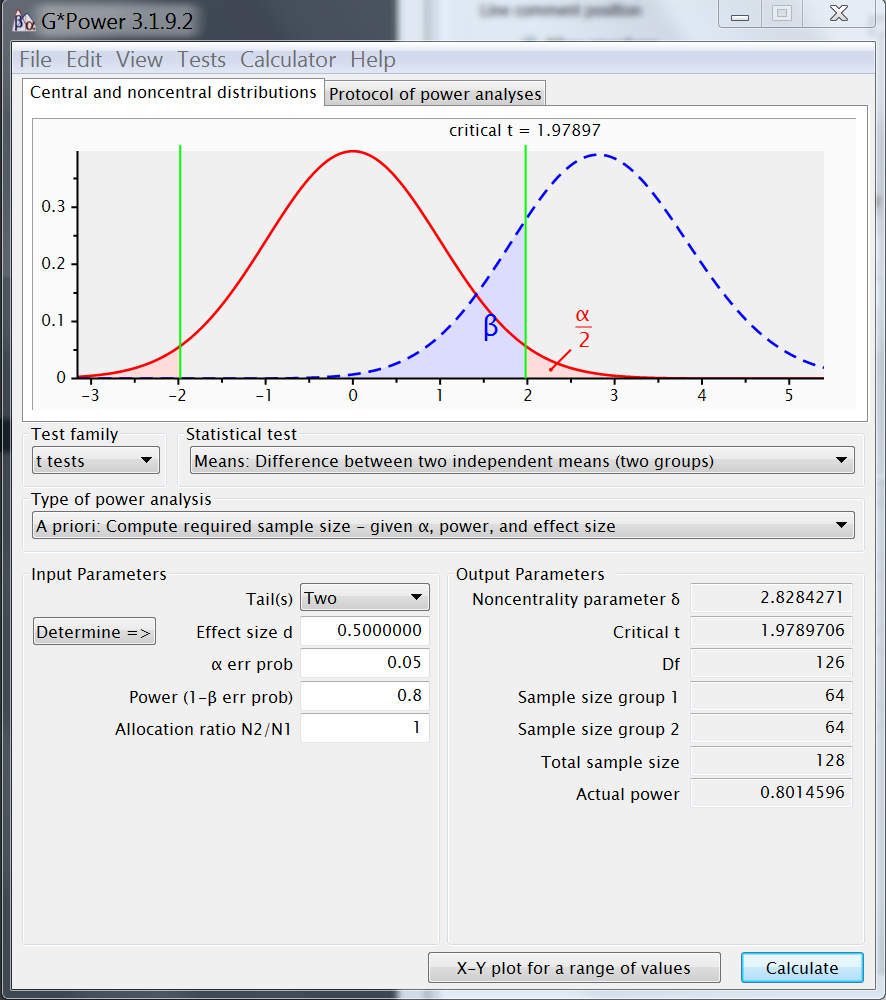
GPower output
~ reference example output- sample size (n) = 64 x 2 = (
128) - degrees of freedom (df) = 126 (128-2)
- critical t = 1.979
- decision boundary given α and df
qt(.975,126)
- decision boundary given α and df
- non centrality parameter ( δ ) = 2.8284
- shift
Ha(true) away fromHo(null)
2/(4*sqrt(2))*sqrt(64)
- shift
- distributions: central + non-central
- power ≥ .80 (1- β) = 0.8015
- sample size (n) = 64 x 2 = (
2:30
The result is 'almost' the same as before, with the normal distribution, but slightly less efficient. The critical t depends on the degrees of freedom (or sample size). The resulting non-centrality parameter (shift) combines effect size and sample size.
SHOW MARKER
GPower protocol
- Summary for future reference or communication
- File/Edit save or print file (copy-paste)
t tests - Means: Difference between two independent means (two groups)
Analysis: A priori: Compute required sample size
Input:
Tail(s) = Two
Effect size d = 0.5000000
α err prob = 0.05
Power (1-β err prob) = .8
Allocation ratio N2/N1 = 1
Output:
Noncentrality parameter δ = 2.8284271
Critical t = 1.9789706
Df = 126
Sample size group 1 = 64
Sample size group 2 = 64
Total sample size = 128
Actual power = 0.8014596
00:30
Maybe convenient is that you can copy-paste the resulting output (and input) into a text file, to communicate to others or yourself later.
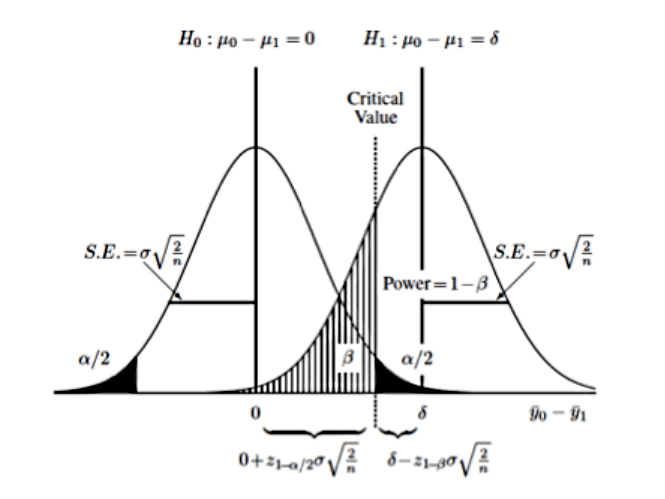
Non-centrality parameter ( δ ), shift Ha from Ho
Hoacts as benchmark → eg., no difference- set cutoff on
Ho ~ t(ncp=0,df)using α, - reject
Hoif test returnsimplausiblevalue
- set cutoff on
Haacts as truth → eg., difference of .5 SDHa ~ t(ncp!=0,df)- δ as violation of
Ho→ shift (location/shape)
δ, the non-centrality parameter
- combines
- assumed
effect size(target or signal) - conditional on
sample size(information)
- assumed
- determines overlap (power ↔ sample size)
- probability beyond cutoff at
Hoevaluated onHa
- probability beyond cutoff at
- combines
4:00
All depends on the difference between the distribution assuming no effect, and the one representing the effect of interest. The shift is quantified by the non-centrality parameter, which combines sample and effect size.
Note: Ho and Ha, asymmetry in statistical testing
Hais NOT interchangeable withHoCut-off at
Housing α- in statistics → observe test statistics (
Haunknown) - in sample size calculation → assume
Ha
- in statistics → observe test statistics (
If fail to reject then remain in doubt
- absence of evidence ≠ evidence of absence
- p-value → P(statistic|
Ho) != P(Ho|statistic) - example: evidence for insignificant η same as for η * 2
- p-value → P(statistic|
- absence of evidence ≠ evidence of absence
Equivalence testing →
Hafor 'no effect'- reject
Hothat smaller than 0 - | Δ | AND bigger than 0 + | Δ | - acts as two superiority tests with margin, combined
- reject
07:00
While simply the difference matters, between Ho and Ha, in statistics they are not the interchangeable. The alternative is just an assumed effect.
Alternative: divide by N
- Constant difference, changing shape
- divide by n: sample size ~ standard deviation
- non-centrality parameter: sample size ~ location
n=(Zα/2+Zβ)2∗2∗σ2d2
n=(−1.96−0.84)2∗2∗4222
n=62.79

2:30
The non-centrality parameter combines effect and sample size, alternatively sample size could be looked at separately. Here the shape changes with growing sample size.
Type I/II error probability
Inference test based on cut-off's (density → AUC=1)
Type I error: incorrectly reject
Ho(false positive):- cut-off at
Ho, error prob. α controlled - one/two tailed → one/both sides informative ?
- cut-off at
Type II error: incorrectly fail to reject
Ho(false negative):- cut-off at
Ho, error prob. β obtained fromHa Haassumed known in a power analyses
- cut-off at
power = 1 - β = probability correct rejection (true positive)
Inference versus truth
- infer: effect exists vs. unsure
- truth: effect exist vs. does not

| infer=Ha | infer=Ho | sum | |
| truth=Ho | `α` | 1- `α` | 1 |
| truth=Ha | 1- `β` | `β` | 1 |
3:00
Inference is based on the cut-off values, and so errors are possible.
Either it is incorrectly after the cut-off, considered from Ho,
or it is incorrectly before the cut-off.
Moving the cut-off makes one error bigger and the other smaller,
but not with equal amounts !
Given a 'truth', the probability sums up to one, you are either right or wrong.
Create plot
- create plot
- X-Y plot for range of values
- Y-axis / X-axis / curves and constant
- assumes calculated analysis
~ reference example
- beware of order !
- plot sample size (y-axis)
- by type I error α (x-axis)
- from .01 to .2 in steps of .01
- for 4 values of power (curves)
- with values .8 in steps of .05
- and assume an effect size (constant)
- .5 from the reference example
- notice Table option
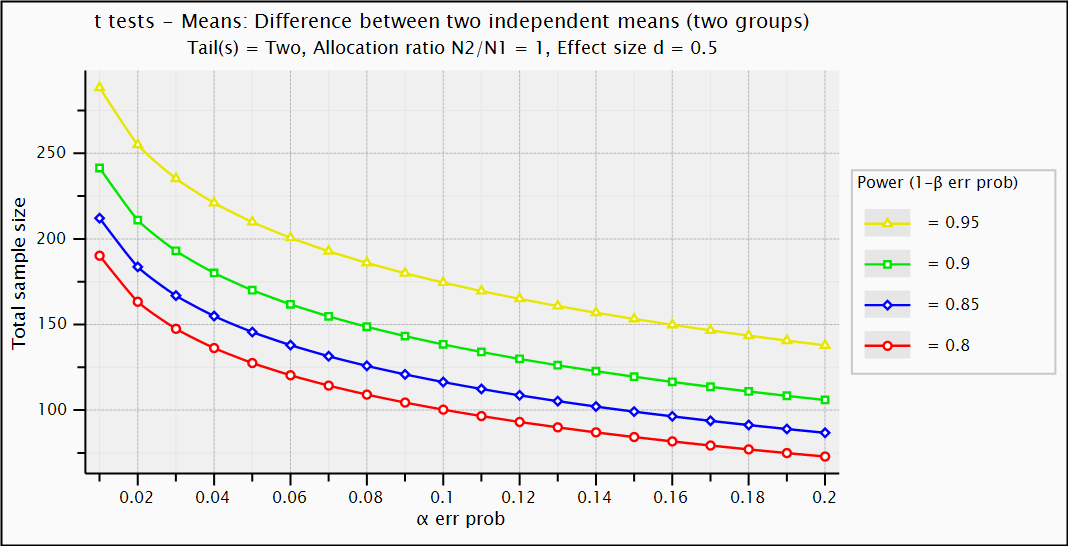
2:00 + 3:00
order is important do it yourself after I did
Exercise on errors, interpret plot
- Understand the building blocks, interpret the plot
- where on the red curve (right)
type II error = 4 * type I error ? - when smaller effect size (.25), what changes ?
- plot power instead of sample size
- with 4 power curves
with sample sizes 32 in step of 32 - what is relation type I and II error ?
- with 4 power curves
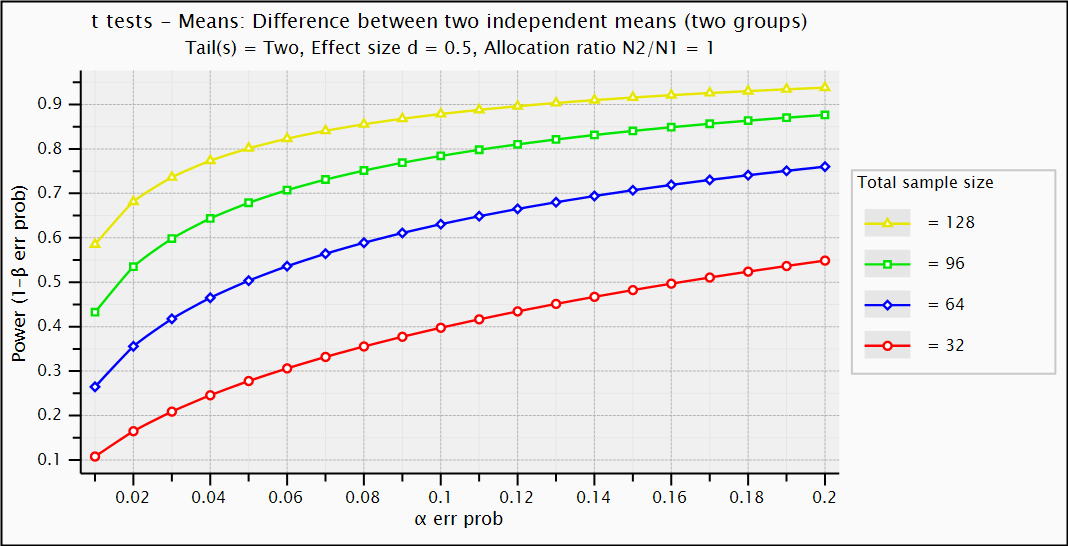
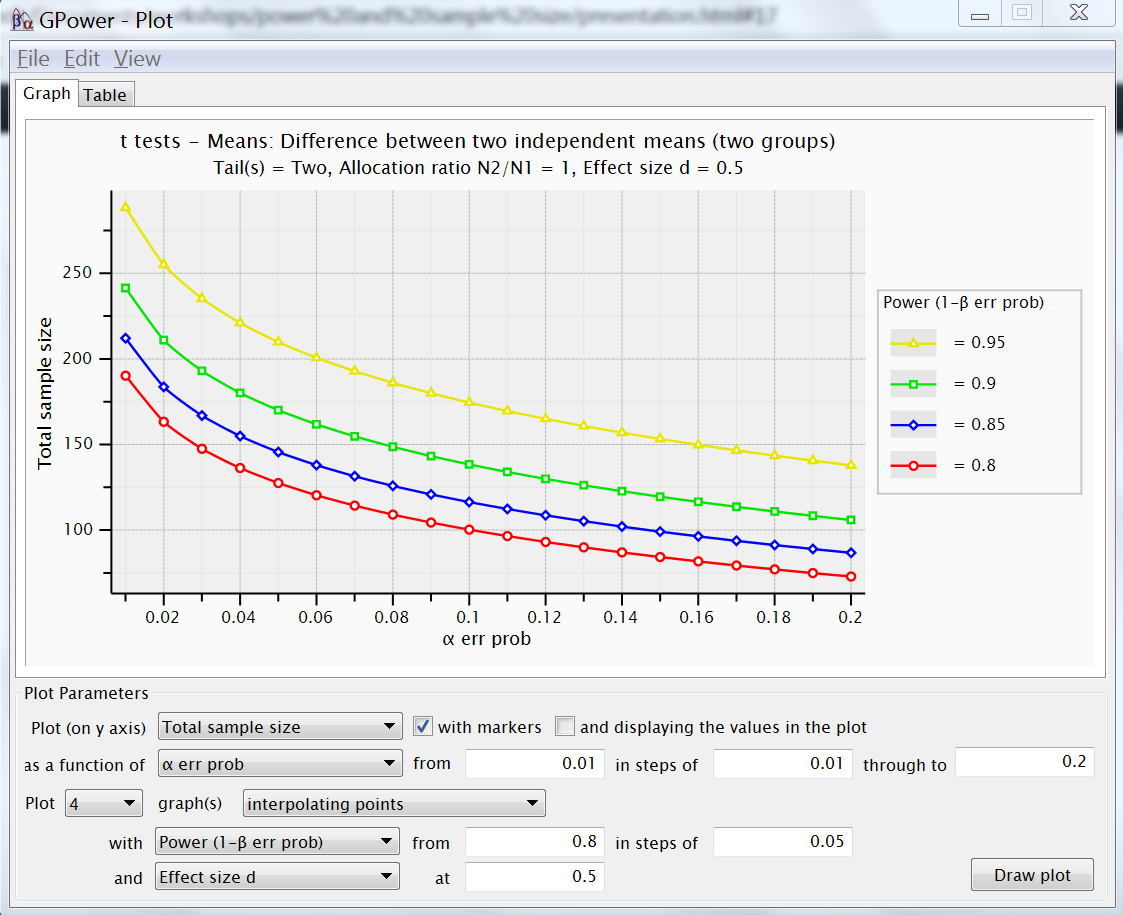
- what would be difference between curves for α = 0 ?
1:00 + 3:00
red is power .8, so type II is .2, divided by 4 is .05 for alpha sample size range changes, change one building block, Y-axis responds, same curves if type I error up, power up, so II down, given the rest, but not all same strength of change if you do not allow for any type I, then power is 0, because infinity on t-distribution
Decide Type I/II error probability
Popular choices
- α often in range .01 - .05 → 1/100 - 1/20
- β often in range .2 to .1 → power = 80% to 90%
α & β inversely related
- power = 1 - β > 1 - 2 * α
- α & β often selected in 1/4 ratio
type I error is 4 times worse !! - which error you want to avoid most ?
- cheap aids test ? → avoid type II
- heavy cancer treatment ? → avoid type I
- probability for errors always exists

2:00
popular choices, in ratios / percentages inversely related, so make a choice what error you want to avoid most look at surfaces, .025 * 8 for .2
Control Type I error
Defined on the Ho, known
- assumes only sampling variability
Multiple testing
- typically used to explore effects in more detail
- inflates type I error α (each peak possible error)
- family of tests: 1−(1−α)k → correct, eg., Bonferroni ( α/k)
Interim analysis
- interim analysis (analyze and conditionally proceed)
- plan in advance
- alpha spending, eg., O'Brien-Flemming bounds
- NOT GPower
- our own simulation tool (Susanne Blotwijk):
http://apps.icds.be/simAlphaSpending/
- our own simulation tool (Susanne Blotwijk):
- determine boundaries with PASS, R (ldbounds), ...
5:00 + 1:00
alpha on the Ho, so under control, assumes variation only due to sampling if multiple tests, each time possible error, prob error at least once increases compensate for multiple testing, 1 minus each time correct, bonferoni is simple way to get that with interim, also multiple testing, make decision, not only sampling, account for that alpha spending, different boundaries with adjusted alphas that total alpha not in Gpower, have a look at susanne
For fun: P(effect exists | test says so)
- Using α, β and power or 1−β
- P(infer=Ha|truth=Ha)=power → P(test says there is effect | effect exists)
- P(infer=Ha|truth=Ho)=α
- P(infer=Ho|truth=Ha)=β
- P(truth_=Ha|infer_=Ha)=P(infer=Ha|truth=Ha)∗P(truth=Ha)P(infer=Ha) → Bayes Theorem
- __ = P(infer=Ha|truth=Ha)∗P(truth=Ha)P(infer=Ha|truth=Ha)∗P(truth=Ha)+P(infer=Ha|truth=Ho)∗P(truth=Ho)
- __ = power∗P(truth=Ha)power∗P(truth=Ha)+α∗P(truth=Ho) → depends on prior probabilities
- IF very low probability model is true (eg., .01) → P(truth=Ha)=.01
- THEN probability effect exists if test says so is low, in this case only .14 !!
- P(truth=Ha|infer=Ha)=.8∗.01.8∗.01+.05∗.99=.14
5:00
Effect sizes, in principle
Estimate/guestimate of minimal magnitude of interest
Typically standardized: signal to noise ratio (noise provides scale)
- eg., effect size d = .5 means .5 standard deviations
- eg., difference on scale of pooled standard deviation
Part of non-centrality (as is sample size) → pushing away
Ha~ practical relevance (not statistical significance)
- NOT p-value ~ partly effect size, but also partly sample size
2 main families of effect sizes (test specific)
d-family(differences) andr-family(associations)- transform one into other, eg., d = .5 → r = .243
d=2r√1−r2 r=d√d2+4 d=ln(OR)∗√3π
4:00
third building block, effect, magnitude standardized so that meaningful to interpret and compare signal to noise ratio, 2/4 = .5, really is .5 standard deviations means, difference on scale of pooled sd's while part of non centrality, does not include sample size statistical significance does include sample size
Vd=4Vr(1−r2)3; Vr=42Vd(d2+4)3; Vd=Vln(OR)∗3π2
Effect sizes, in literature
- Cohen, J. (1992). A power primer. Psychological Bulletin, 112, 155–159.
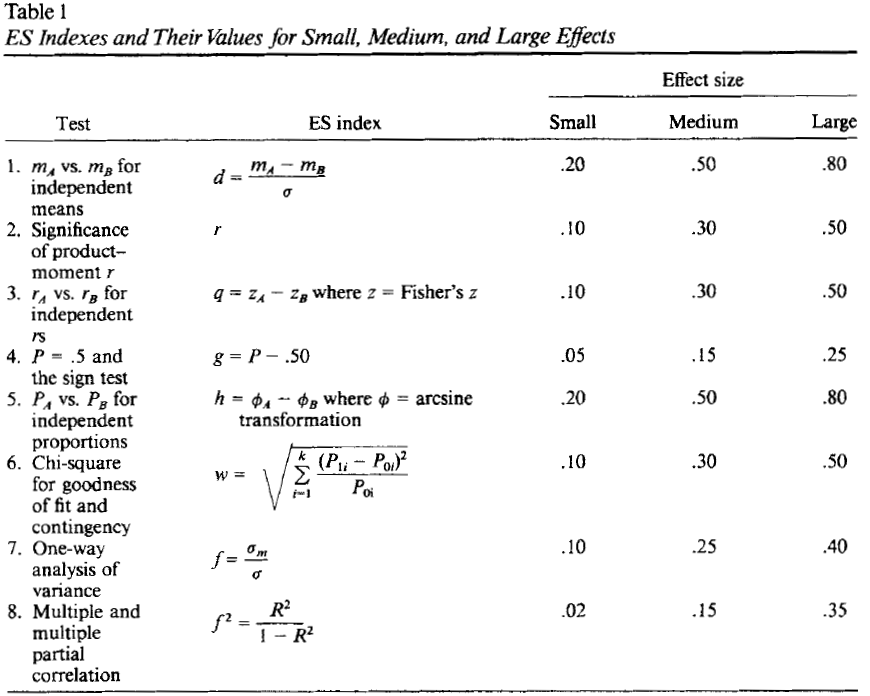
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed).
- famous Cohen conventions but beware, just rules of thumb
- more than 70 different effect sizes... most of them related
- Ellis, P. D. (2010). The essential guide to effect sizes: statistical power, meta-analysis, and the interpretation of research results.

1:00
Effect sizes, in GPower (Determine)
Effect sizes are test specific
- t-test → group means and sd's
- one-way anova →
variance explained & error - regression →
sd's and correlations - . . . .
GPower helps with
Determine- sliding window
- one or more effect size specifications
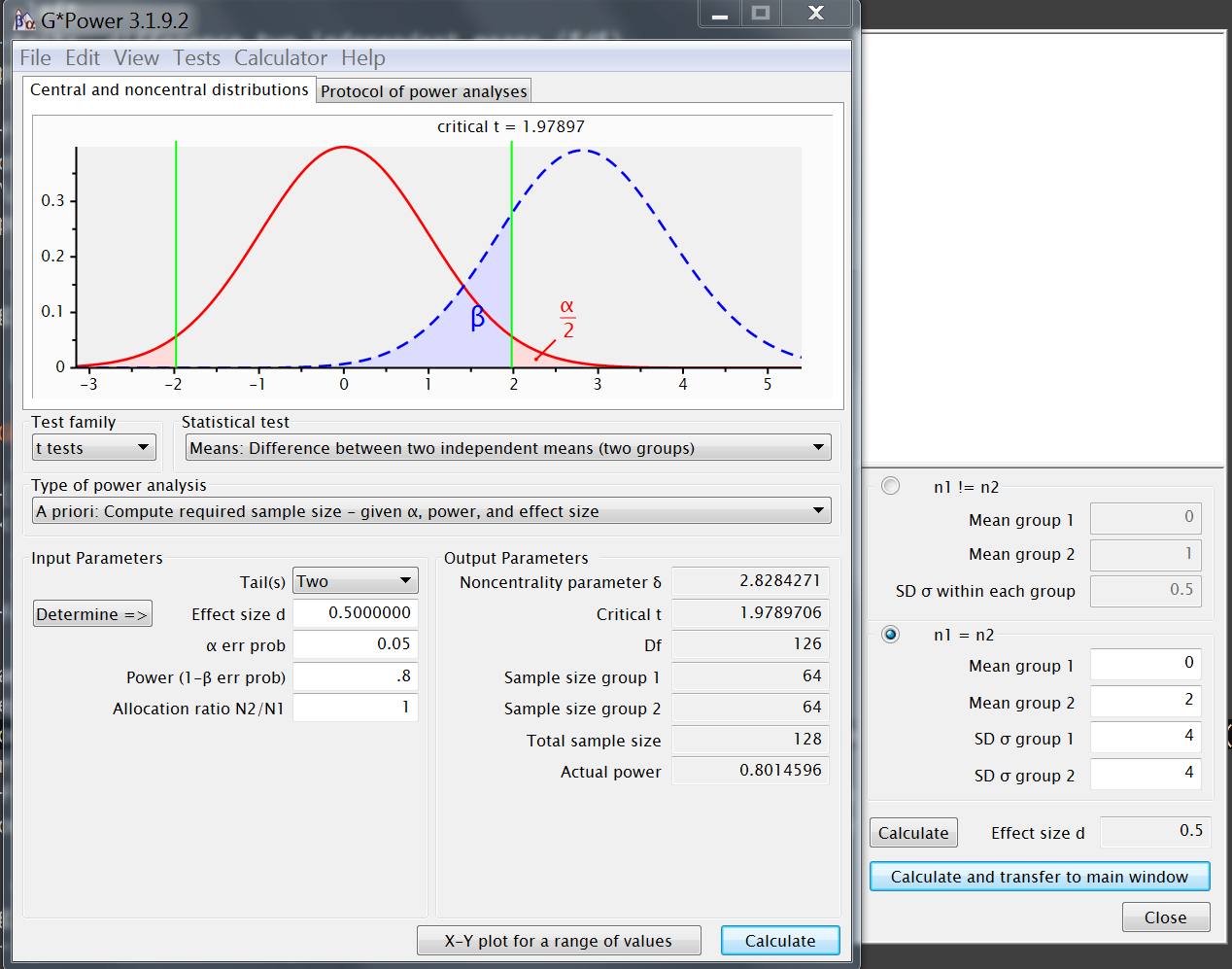
GPOWER t-f-r-... the determine button opens a window to help specify the effects size given certain values, others are calculated and transferred to the main window
Exercise on effect sizes, ingredients Cohen's d
- For the
reference example:- change mean values from 0 and 2 to 4 and 6, what changes ?
- change sd values to 2 for each, what changes ?
- effect size ?
- total sample size ?
- critical t ?
- non-centrality ?
- change sd values to 8 for each, what changes ?
- change sd to 2 and 5.3, or 1 and 5.5,
how does it compare to 4 and 4 ?
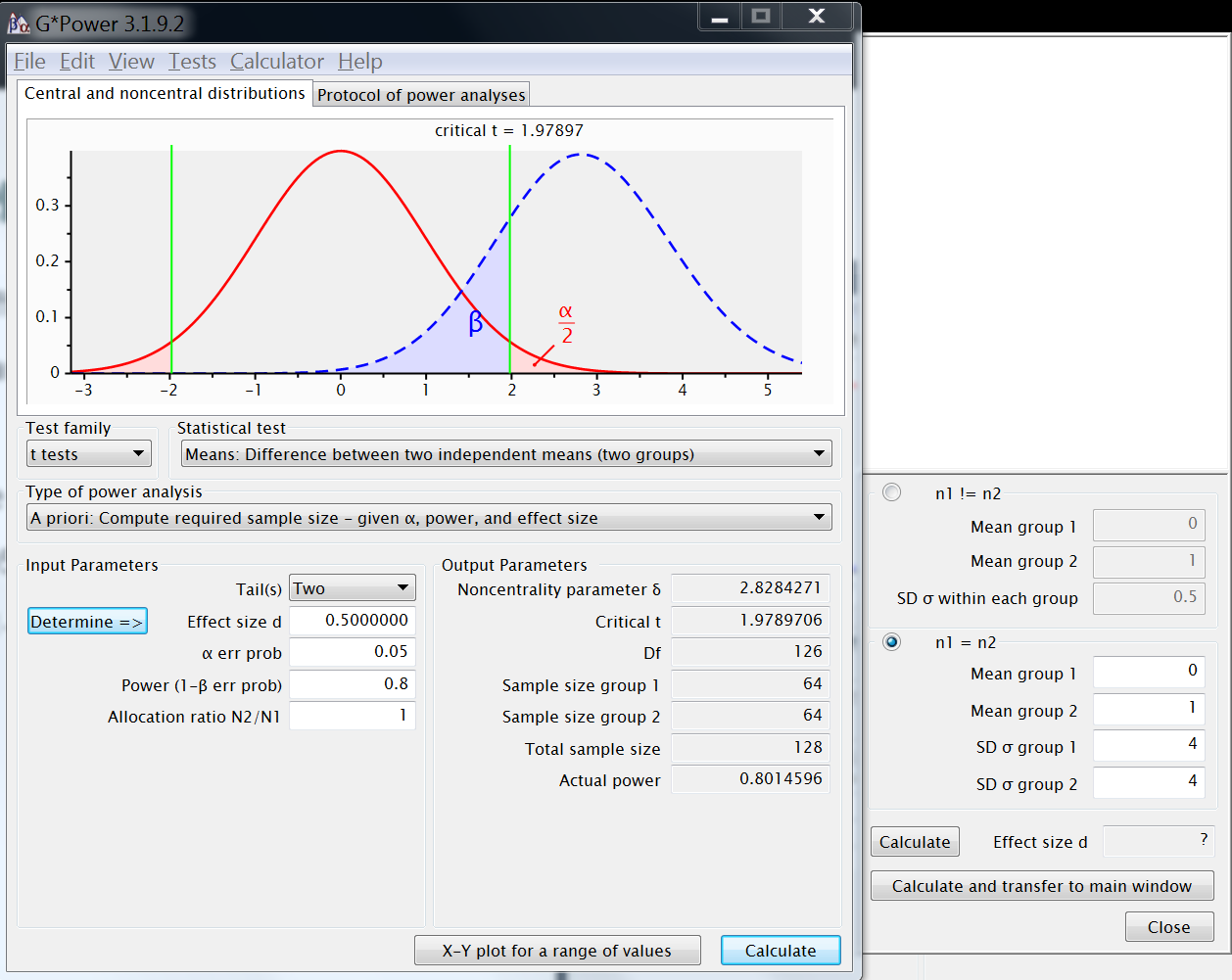
d = standardized difference less noise, better signal to noise ratio effect size bigger, less sample size THUS slightly larger t cut off no clear relation with ncp because effect size + sample size - more noise, opposite with difference in sd, bigger has more impact, much lower compensates a bit higher
Exercise on effect sizes, plot
- For the
reference example:- plot powercurve: power by effect size
- compare 6 sample sizes: 34 in steps of 34
- for a range of effect sizes in between .2 and 1.2
- use α equal to .05
- pinpoint the situations from previous section on the plot (sd=4 and 2).
- how does power change when doubling the effect size ?
- powercurve → X-Y plot for range of values
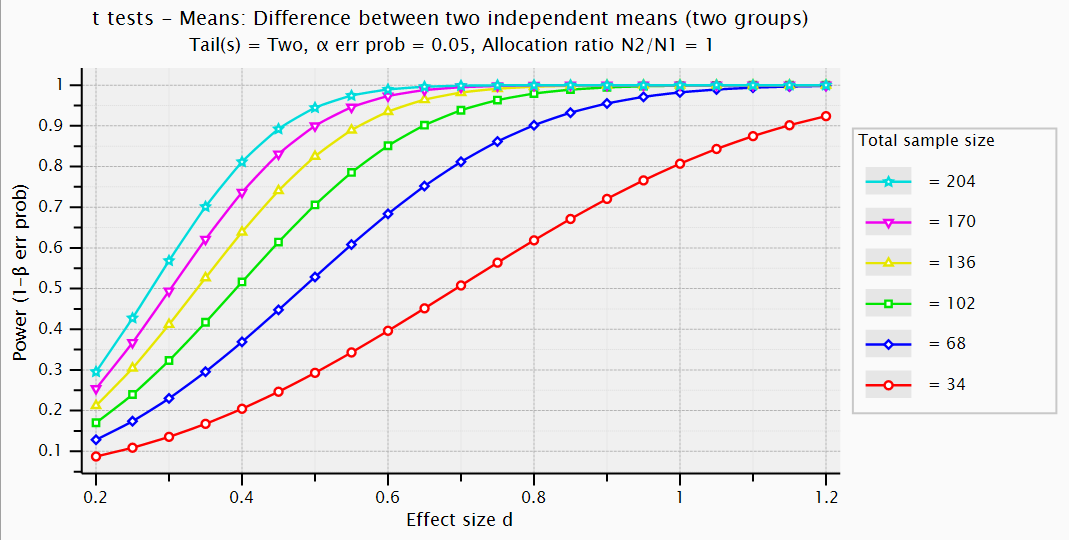
power by effect size, beware of changes after including the 6 power curves effect sizes .2 to 1.2, in steps of whatever, maybe .1 the sd 4 situation, comes with 64 observations, blue, effect size .5 the sd 2, is effect size 1 on 34, red doubling the effect size shows increase in power, but not for all the same
Exercise on effect size, imbalance
For the
reference example:- compare for allocation ratios 1, .5, 2, 10, 50
- repeat for effect size 1, and compare
? no idea why n1 ≠ n2

after calculate plot, to change allocation ratio
allocation of /2 or *2 is same, just largest group differs, and can differ if standard deviations differ but does not show, so, maybe not OK effect size does not influence the increase much (multiplication)
2 10 18 28 50 38 98 160 238 412 144 382 632 955 1638
Effect sizes, how to determine them in theory
Choice of effect size matters → justify choice !!
Choice of effect size depends on aim of the study
- realistic (eg., previously observed effect) → replicate
- important (eg., minimally relevant effect)
- NOT significant → meaningless, dependent on sample size
Choice of effect size dependent on statistical test of interest
- for independent t-test → means and standard deviations
- possible alternative: variance explained, eg., 1 versus 16+1
- with one-way ANOVA ( f = .25 instead of d = .5)
- with linear regression ( f2 = .0625 instead of d = .5)
- https://www.psychometrica.de/effect_size.html#transform
the most important is importance, if you know what matters, you can power your study to detect that usually just go to literature, find what already found, ensures realistic values, but not necessarily relevant ones never use significance itself, it is meaningless, it depends on sample size and is therefore not an effect size.
also here, one effect size can be transformed into the next, d to f, to f2 many more transformations at psychometrica
Effect sizes, how to determine them in practice
Experts / patients → use if possible → importance
minimally clinically relevant effectLiterature (earlier study / systematic review) → beware of publication bias → realistic
Pilot → guestimate dispersion estimate (not effect size → small sample)
Internal pilot → conditional power (sequential)
Guestimate uncertainty...
- sd from assumed range, assume normal and divide by 6
- sd for proportions at conservative .5
- sd from control, assume treatment the same
...
Turn to Cohen → use if everything else fails (rules of thumb)
- eg., .2 - .5 - .8 for Cohen's d
easier said than done, often it is and remains difficult you can ask experts or patients even, for example to get a pain threshold literature, ok, if it is relevant, but maybe a bit over optimistic a pilot can help to get an idea of the dispersion, not the effect because too few data an internal pilot is possible, maybe get an estimate of the sd along the way to re-calibrate or just try your best to guess, maybe from an assumed range ? avoid rules of thumb of cohen
Relation sample & effect size, type I & II errors
Building blocks:
- sample size ( n )
- effect size ( Δ )
- alpha ( α )
- power ( 1−β )
each parameter
conditional on others
- GPower → type of power analysis
- Apriori: n
~α,power, Δ - Post Hoc:
power~α, n, Δ - Compromise:
power, α~β/α, Δ, n - Criterion: α
~power, Δ, n - Sensitivity: Δ
~α,power, n
- Apriori: n

All four building blocks combined, and one obtained based on the others. So far, worked with apriori, to get the sample size. But also popular, to get the power, then you need alpha, n and delta, (post hoc) OR the relation between alpha and beta (compromise) Not sure why you would extract alpha, this is typically under control but you could use delta, often done, but maybe not always ok, see what effect size is possible with the available data.
Exercise on type of power analysis
- For the
reference example:- retrieve power given n, α and Δ
- then, for power .8, take half the sample size, how does Δ change ?
- then, set β/ α ratio to 4, what is α & β ? what is the critical value ?
- then, keep β/ α ratio to 4 for effect size .7, what is α & β ? critical value ?
power for the reference was .8, we find it as such with half the size of sample, the effect size goes up a bit .5 to .7714 when using a ratio, it is .1 and .4, or .05 and .2,
- use post-hoc 64x2 → .8
- then, for power .8, take half the sample size, how does Δ change ?
- use sensitivity 32x2 (d=.7114)
- Δ from .5 to .7115 = .2115
- bigger effect Δ compensates loss of sample size n
- then, set β / α ratio to 4, what is α & β ? what is the critical value ?
- use compromise 32x2
- α =.09 and β =.38, critical value 1.6994
- then, keep β / α ratio to 4 for effect size .7
- use compromise 32x2
- α =.05 and β =.2, critical value 1.9990
Solution for type of power analysis
- For the
reference example:- retrieve power given n, α and Δ of
referencecase- use post-hoc 64x2 → .8
- then, for power .8, take half the sample size, how does Δ change ?
- use sensitivity 32x2 (d=.7114)
- Δ from .5 to .7115 = .2115
- bigger effect Δ compensates loss of sample size n
- then, set β / α ratio to 4, what is α & β ? what is the critical value ?
- use compromise 32x2
- α =.09 and β =.38, critical value 1.6994
- then, keep β / α ratio to 4 for effect size .7
- use compromise 32x2
- α =.05 and β =.2, critical value 1.9990
- retrieve power given n, α and Δ of
Getting your hands dirty

# calculatorm1=0;m2=2;s1=4;s2=4alpha=.025;N=128var=.5*s1^2+.5*s2^2d=abs(m1-m2)/sqrt(2*var)*sqrt(N/2)tc=tinv(1-alpha,N-1)power=1-nctcdf(tc,N-1,d)
- in
R- qt → get quantile on
Ho( Z1−α/2 ) - pt → get probability on
Ha(non-central)
- qt → get quantile on
.n <- 64.df <- 2*.n-2.ncp <- 2 / (4 * sqrt(2)) * sqrt(.n).power <- 1 - pt( qt(.975,df=.df), df=.df, ncp=.ncp ) - pt( qt(.025,df=.df), df=.df, ncp=.ncp)round(.power,4)## [1] 0.8015You can calculate in Gpower, but, why would you do that. In R, get the cutoff on Ho, get probability on Ha, simple The two sided, has one side almost 0
GPower, beyond the independent t-test
So far, comparing two independent means
From now on, selected topics beyond independent t-test
with small exercises- dependent instead of independent
- non-parametric instead of assuming normality
- relations instead of groups (regression)
- correlations
- proportions, dependent and independent
- more than 2 groups (compare jointly, pairwise, focused)
- more than 1 predictor
- repeated measures
Look into GPower manual
27 tests → effect size, non-centrality parameter and example !!
Dependence between groups
If 2 dependent groups (eg., before/after treatment) → account for correlations
Correlation typically obtained from pilot data, earlier research
GPower: matched pairs (t-test / means, difference 2 dependent means)
- use
reference example,
assume correlation .5 to compare with reference effect size, ncp, n !? - how many observations if no correlation exists (think then try) ? effect size ?
- what changes with correlation .875 (think: more or less n, higher or lower effect size) ?
- what would the power be with the reference sample size, n=128, but now cor=.5 ?
- use
- GPower: matched pairs (t-test / means, difference 2 dependent means)
- Assume correlation .5 to compare with reference effect size, ncp, n
- Δ looks same, n much smaller = 34 (note: 34 x 2)
- different type of effect size: dz ~ d / √2∗(1−ρ)
- How many observations if no correlation exists (think then try) ? effect size ?
- 65, approx. same as INdependent means → 64 (*2=128) but also estimate the correlation
- Δ = dz = .3535 (~ d = .5)
- What changes with correlation .875 (think: more or less n, higher or lower effect size) ?
- effect size * 2 → sample size from 34 to 10 (almost / 4)
- What would the power be with the reference sample size, correlation .5 ? what is the ncp ?
- post - hoc power, 64 * 2 measurements, with .5 correlation
- power > .976, ncp > 4,
Solution for dependence between groups
- GPower: matched pairs (t-test / means, difference 2 dependent means)
- Assume correlation .5 to compare with reference effect size, ncp, n
- Δ looks same, n much smaller = 34 (note: 34 x 2)
- different type of effect size: dz ~ d / √2∗(1−ρ)
- How many observations if no correlation exists (think then try) ? effect size ?
- 65, approx. same as INdependent means → 64 (*2=128) but also estimate the correlation
- Δ = dz = .3535 (~ d = .5)
- What changes with correlation .875 (think: more or less n, higher or lower effect size) ?
- effect size * 2 → sample size from 34 to 10 (almost / 4)
- What would the power be with the reference sample size, correlation .5 ? what is the ncp ?
- post - hoc power, 64 * 2 measurements, with .5 correlation
- power > .976, ncp > 4,
Non-parametric distribution
Expect non-normally distributed residuals, not possible to avoid (eg., transformations)
Only considers ranks or uses permutations → price is efficiency and flexibility
Requires parent distribution (alternative hypothesis), 'min ARE' should be default
GPower: two groups → Wilcoxon-Mann-Whitney (t-test / means, diff. 2 indep. means)
- use
reference example
with normal parent distribution, how much efficiency is lost ? - for a parent distribution 'min ARE', how much efficiency is lost ?
- use
- GPower: two groups → Wilcoxon-Mann-Whitney (t-test / means, diff. 2 indep. means)
- Use
reference example, with normal parent distribution, how much efficiency is lost ?- requires a few more observations (3 more per group), assume normal but based on ranks
- less than 5 % loss (~134/128)
- For a parent distribution 'min ARE', how much efficiency is lost ?
- requires several more observations
- more than 15 % loss (~148/128)
- min ARE is safest choice without extra information, least efficient
Solution for non-parametric distribution
- GPower: two groups → Wilcoxon-Mann-Whitney (t-test / means, diff. 2 indep. means)
- Use
reference example, with normal parent distribution, how much efficiency is lost ?- requires a few more observations (3 more per group)
- less than 5 % loss (~134/128)
- For a parent distribution 'min ARE', how much efficiency is lost ?
- requires several more observations
- more than 15 % loss (~148/128)
- min ARE is safest choice without extra information, least efficient
A relations perspective, regression analysis
Differences between groups → relation observations & grouping (categorization)
Example → d = .5 → r = .243 (note: slope β=r∗σy/σx)
- .243*sqrt( 42+1 )/sqrt( .25 ) = 2
- note: total variance = residual variance + model variance (2 or 0 for all observations)
var((2-1),(0-1),(2-1),(0-1),...) - note: design variance = variance -.5 and .5 for all observations
var((1-.5),(0-.5),(1-.5),(0-.5),...)
- GPower: regression coefficient (t-test / regression, one group size of slope)
- determine slope β and σy for reference values, d=.5 (hint:d~r), SD = 4 and σx = .5 (1/0)
- calculate sample size
- what happens with slope and sample size if predictor values are taken as 1/-1 ?
- determine σy for slope 6, σx = .5, and SD = 4, would it increase the sample size ?
- GPower: regression coefficient (t-test / regression, one group size of slope)
- Determine slope β and σy for reference values, d=.5, SD = 4 and σx = .5 (1/0)
- σx = √.25 = .5 (binary, 2 groups: 0 and 1) → slope = 2, σy = 4.12 = √42+12
- Calculate sample size
- 128, same as for reference example, now with effect size slope H1 given 1/0 predictor values
- What happens with slope and sample size if predictor values are taken as 1/-1 ?
- β is 1, a difference of 2 over 2 units instead of 1
- no difference in sample size, compensated by variance of design
- Determine σy for slope 6, σx = .5, and SD = 4, would it increase the sample size ?
- σy = 5 = √42+32 (assuming balanced data)
- bigger effect → smaller sample size, only 17
Solution on a relations perspective
- GPower: regression coefficient (t-test / regression, one group size of slope)
- Determine slope β and σy for reference values, d=.5, SD = 4 and σx = .5 (1/0)
- σx = √.25 = .5 (binary, 2 groups: 0 and 1) → slope = 2, σy = 4.12 = √42+12
- Calculate sample size
- 128, same as for reference example, now with effect size slope H1 given 1/0 predictor values
- What happens with slope and sample size if predictor values are taken as 1/-1 ?
- β is 1, a difference of 2 over 2 units instead of 1
- no difference in sample size, compensated by variance of design
- Determine σy for slope 6, σx = .5, and SD = 4, would it increase the sample size ?
- σy = 5 = √42+32 (assuming balanced data)
- bigger effect → smaller sample size, only 17
A variance ratio perspective, ANOVA
Difference between groups or relation → ratio between and within group variance
GPower: regression coefficient (t-test / regression, fixed model single regression coef)
- use
reference example, regression style (sd of effect and error, but squared) - calculate sample size, compare effect sizes ?
- what if also other predictors in the model ?
- what if 3 predictors extra reduce residual variance to 50% ?
- use
Note:
- partial R2 = variance predictor / total variance
- f2 = variance predictor / residual variance = R2/(1−R2)
- GPower: regression coefficient (t-test / regression, fixed model single regression coef)
- use
reference example, regression style (sd of effect and error, but squared)
- use
- Calculate sample size, compare effect sizes ?
- 128, same as for reference example, now with f2 = .252 = .0625 (d=.5,r=.243)
- What if also other predictors in the model ?
- very little impact → loss of degree of freedom
- ignore that predictors explain variance → reduce residual variance
- What if 3 predictors extra reduce residual variance to 50% ?
- control for confounding variables: less noise → bigger effect size
- sample size much less (65)
Solution on a variance ratio perspective
- GPower: regression coefficient (t-test / regression, fixed model single regression coef)
- use
reference example, regression style (sd of effect and error, but squared)
- use
- Calculate sample size, compare effect sizes ?
- 128, same as for reference example, now with f2 = .252 = .0625 (d=.5,r=.243)
- What if also other predictors in the model ?
- very little impact → loss of degree of freedom
- ignore that predictors explain variance → reduce residual variance
- What if 3 predictors extra reduce residual variance to 50% ?
- control for confounding variables: less noise → bigger effect size
- sample size much less (65)
A variance ratio perspective on multiple groups
Multiple groups → not one effect size
dF-test statistic & effect size
f, ratio of variances σ2between/σ2withinσ2between = variance between groups differences
σ2within = variance within group differences
Example: one control and two treatments
reference example+ 1 group- sd within each group, for all groups (C,T1,T2) = 4
- means C=0, T1=2 and for example T2=4
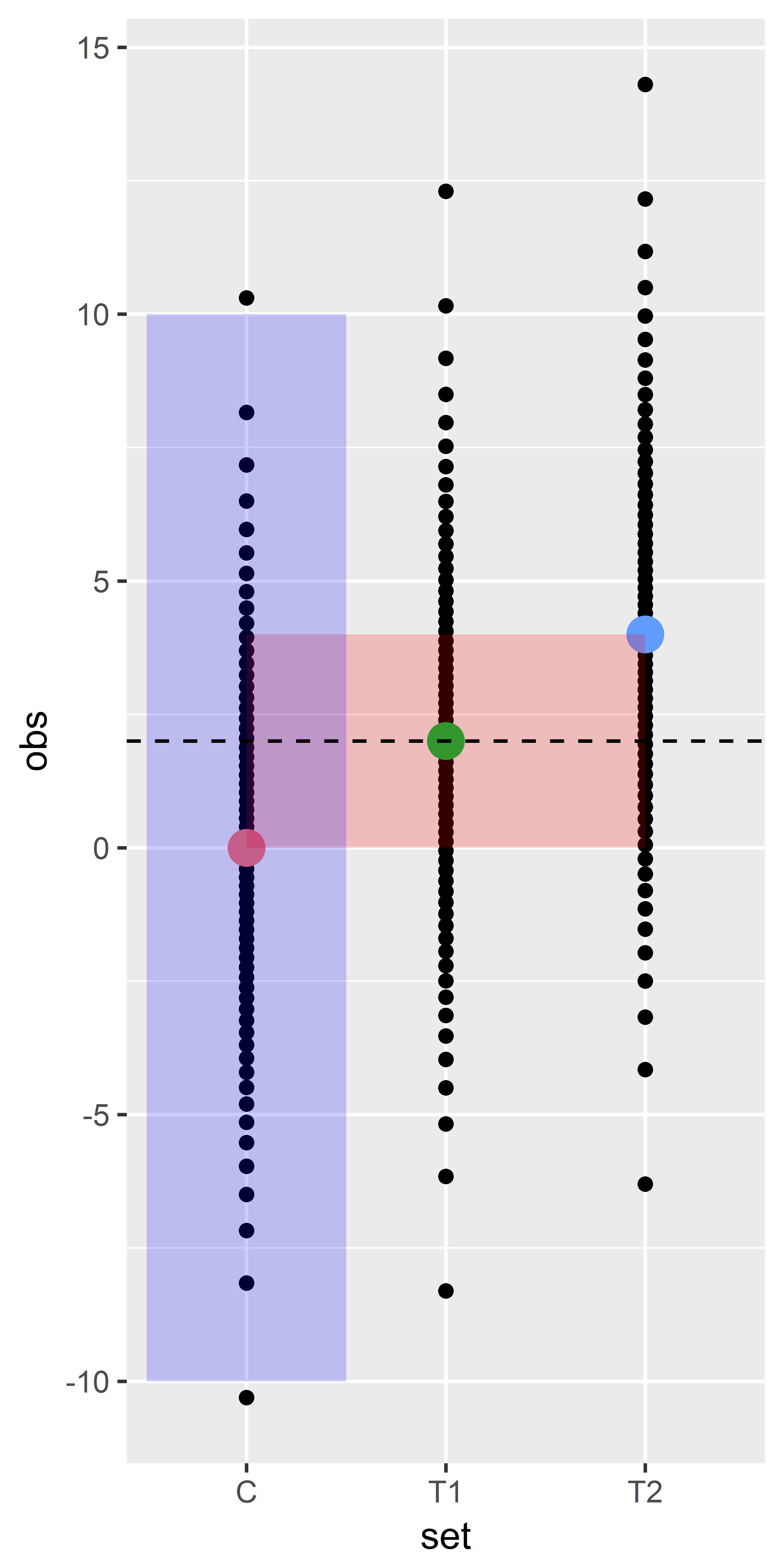
Multiple groups: omnibus
Difference between some groups → at least two differ
GPower: one-way Anova (F-test / Means, ANOVA - fixed effects, omnibus, one way)
- effect size f, with numerator/denominator df
- obtain sample size for
reference example, just 2 groups C and T1 (size=64)! - play with sizes, how does size matter ?
- include third group, with mean 2, what are sample sizes (compare with 2 groups)?
- set third group mean to 0, how does it compare with mean 2 (think and try)?
- set third group mean to 4, but also vary middle group (eg., 1 or 3), does that have an effect ?
- change procedure: repeat for between variance 2.67 (balanced: 0, 2, 4) and within variance 16 ?
- GPower: one-way Anova (F-test / Means, ANOVA - fixed effects, omnibus, one way)
- Obtain sample size for
reference example, just 2 groups C and T1 (size=64)!- 128, same again, despite different effect size (f) and distribution
- size used only to include imbalance
- Include third group, with mean 2, what are sample sizes (compare with 2 groups)?
- effect sizes f = .236; sample size 177 (59*3), requires more observations
- Set third group mean to 0, how does it compare with mean 2 (think and try)?
- effect and sample size same, no difference whether big 0 group or big 2 group.
- Set third group mean to 4, but also vary middle group (eg., 1 or 3), does that have an effect ?
- effect sizes f = .408 (4), .425 (1/3), increase with middle group away from middle.
- Change procedure: repeat for between variance 2.67 (balanced: 0, 2, 4) and within variance 16 ?
- sample size 21*3=63, for f = .408 (1/7th explained = 1 between / 6 within)
Solution for multiple groups omnibus
- GPower: one-way Anova (F-test / Means, ANOVA - fixed effects, omnibus, one way)
- Obtain sample size for
reference example, just 2 groups C and T1 (size=64)!- 128, same again, despite different effect size (f) and distribution
- size used only to include imbalance
- Include third group, with mean 2, what are sample sizes (compare with 2 groups)?
- effect sizes f = .236; sample size 177 (59*3), requires more observations
- Set third group mean to 0, how does it compare with mean 2 (think and try)?
- effect and sample size same, no difference whether big 0 group or big 2 group.
- Set third group mean to 4, but also vary middle group (eg., 1 or 3), does that have an effect ?
- effect sizes f = .408 (4), .425 (1/3), increase with middle group away from middle.
- Change procedure: repeat for between variance 2.67 (balanced: 0, 2, 4) and within variance 16 ?
- sample size 21*3=63, for f = .408 (1/7th explained = 1 between / 6 within)
Multiple groups: pairwise
Assume one control, and two treatments
- interested in all three pairwise comparisons → maybe Tukey
- typically run aposteriori, after omnibus shows effect
- use multiple t-tests with corrected α for multiple testing
GPower: t-tests/means difference two independent groups
- interested in all three pairwise comparisons → maybe Tukey
Apply Bonferroni correction for original 3 group example (0, 2, 4)
- what samples sizes are necessary for all three pairwise tests ?
- what if biggest difference ignored (C-T2), because know that easier to detect ?
- with original 64 sized groups, what is the power to detect a difference group (C-T1) (both situations above) ?
- GPower: t-tests/means difference two independent groups
- Apply Bonferroni correction for original 3 group example (0, 2, 4)
- What samples sizes are necessary for all three pairwise tests ?
- 0-2 and 2-4 → d=.5, 0-4 → d=1
- divide α by 3 → .05/3=.0167
- sample size 86 2 for 0-2 and 2-4, 23 2 for 0-4 → 86 * 3 = 258
- What if biggest difference ignored (C-T2), because know that easier to detect ?
- divide α by 2 → .05/2=.025
- sample size 78 2 for 0-2 and 2-4 → 78 3 = 234 (24 less)
- With original 64 sized groups, what is the power (both situations above) ?
- .6562 for 3 tests ( α =.0167)
- .7118 for 2 tests ( α =.0250)
- post-hoc test → power-loss (lower α → higher β)
Solution for multiple groups pairwise
- GPower: t-tests/means difference two independent groups
- Apply Bonferroni correction for original 3 group example (0, 2, 4)
- What samples sizes are necessary for all three pairwise tests ?
- 0-2 and 2-4 → d=.5, 0-4 → d=1
- divide α by 3 → .05/3=.0167
- sample size 86 2 for 0-2 and 2-4, 23 2 for 0-4 → 86 * 3 = 258
- What if biggest difference ignored (C-T2), because know that easier to detect ?
- divide α by 2 → .05/2=.025
- sample size 78 2 for 0-2 and 2-4 → 78 3 = 234 (24 less)
- With original 64 sized groups, what is the power (both situations above) ?
- .6562 for 3 tests ( α =.0167)
- .7118 for 2 tests ( α =.0250)
- post-hoc test → power-loss (lower α → higher β)
Multiple groups: contrasts
Contrasts are linear combinations → planned comparison
- eg., 1∗T1−1∗C≠0 & 1∗T2−1∗C≠0
- eg., .5∗(1∗T1+1∗T2)−1∗C≠0
Effect sizes for planned comparisons must be calculated !!
- variance ratios (between / within)
- standard deviation of contrasts → between variance
Each contrast
- uses 1 degree of freedom
- combines a specific number of levels
Multiple testing correction may be appropriate
group means μi
pre-specified coefficients ci
sample sizes ni
total sample size N
σcontrast=|∑μi∗ci|√N∑kic2i/ni
Multiple groups: contrasts (continued)
GPower: one-way ANOVA (F-test / Means, ANOVA-fixed effects,special,main,interaction)
Obtain effect sizes for contrasts (assume equally sized for convenience)
- σcontrast T1-C: (−1∗0+1∗2+0∗4)√(2∗((−1)2+12+02))=1; σerror = 4 → f=.25
- σcontrast T2-C: (−1∗0+0∗2+1∗4)√(2∗((−1)2+02+12))=2; σerror = 4 → f=.5
- σcontrast (T1+T2)/2-C: (−1∗0+(1/2)∗2+(1/2)∗4)√(3∗((−1)2+(1/2)2+(1/2)2))=1.414214; σerror = 4 → f=.3535
Sample size for each contrast, each 1 df
- what samples sizes for either contrast 1 or contrast 2 ?
- what samples sizes for both contrast 1 and contrast 2 combined ?
- if taking that sample size, what will be the power for T1-T2 ?
- what samples size for contrast 3 ?
- GPower: one-way ANOVA (F-test / Means, ANOVA-fixed effects,special,main,interaction)
- What samples sizes for either contrast 1 or contrast 2 ?
- variance explained 12 or 22
- for T1-C f = √12/42 = .25 = d/2 → 128 (64 C - 64 T1)
- for T2-C f = √22/42 = .50 = d/2 → 34 (17 C - 17 T2)
- What samples sizes for both contrast 1 and contrast 2 combined ?
- multiple testing, consider Bonferroni correction → /2
- for T1-C 155, for T2-C 41 → total 175 (78 C, 77 T1, 20 T2)
- If taking that sample size, what will be the power for T1-T2 ?
- post-hoc, 77 and 20, with d=.5 and α = .5 → power ≈ .5
- What samples size for contrast 3 ?
- variance contrast 1.41422
- 3 groups, little impact if any
- for .5*(T1+T2) - C f = √2/16 = .3535 → 65 (22 C, 21 T1, 22 T2)
Solution for multiple groups contrasts
- GPower: one-way ANOVA (F-test / Means, ANOVA-fixed effects,special,main,interaction)
- What samples sizes for either contrast 1 or contrast 2 ?
- variance explained 12 or 22
- for T1-C f = √12/42 = .25 = d/2 → 128 (64 C - 64 T1)
- for T2-C f = √22/42 = .50 = d/2 → 34 (17 C - 17 T2)
- What samples sizes for both contrast 1 and contrast 2 combined ?
- multiple testing, consider Bonferroni correction → /2
- for T1-C 155, for T2-C 41 → total 175 (78 C, 77 T1, 20 T2)
- If taking that sample size, what will be the power for T1-T2 ?
- post-hoc, 77 and 20, with d=.5 and α = .5 → power ≈ .5
- What samples size for contrast 3 ?
- variance contrast 1.41422
- 3 groups, little impact if any
- for .5*(T1+T2) - C f = √2/16 = .3535 → 65 (22 C, 21 T1, 22 T2)
Multiple factors
Multiple main effects and possibly interaction effects (eg., treatment and type)
- main effects (average effects, additive) & interaction (factor level specific effects)
- note: numerator degrees of freedom → main effect (nr-1), interaction (nr1-1)*(nr2-1)
- η2 = f2/(1+f2), remember f=d/2 for two groups
- note: get effect sizes for two way anova: http://apps.icds.be/effectSizes/
GPower: multiway ANOVA (F-test / Means, ANOVA-fixed effects,special,main,interaction)
- determine η2 and sample size for
reference example,
remember the between group variance ? - use the app: use for means only values 0 and 2, and 4 and 6 if necessary
for treatment use C-T1-T2, for type (second predictor) use B1-B2- get η2 for treatment effect but no type effect ? recognize f ?
- specify such that types differ, not treatment → f and sample size ?
- specify such that treatment effect only for one type → f and sample size ?
- specify effect for both treatment and type, without interaction → f and sample size ?
- determine η2 and sample size for
- GPower: multiway ANOVA (F-test / Means, ANOVA-fixed effects,special,main,interaction)
- Determine sample size for
reference example,
remember the between group variance ?- between group variance 1, within 16, sample size 128 (numerator df = 2-1)
- 2 x 2 with 0-2 → η2 as expected = .0588
- Get η2 for treatment effect but no type effect ? recognize f ?
- 0-2-4 for both types → f = .4082 of the omnibus F-test (compare all groups)
- Specify such that types differ, not treatment → f and sample size ?
- 0-0-0 versus 2-2-2 → f = .25 of t-test (compare two groups)
- Specify such that treatment effect only for one type → f and sample size ?
- 0-2-4 versus 0-0-0 → f = .2041, .25 and .2041
- detect interaction (num df = 2) = 235 total (40 per combination)
- detect only treatment effect (num df = 2) = 235 total (79 each group, 79/2 per combination)
- detect only type effect (num df = 1) = 128 total (64 each group, 64/3 per combination)
- detect both both main effects = 40 each combination ~ max(79/2,64/3)
- 0-2-4 versus 0-0-0 → f = .2041, .25 and .2041
- Specify effect for both treatment and type, without interaction → f and sample size ?
- 0-2-4 versus 2-4-6 → f = .4082, .25 and 0, sample size = 21 per combination
Solution for multiple factors
- GPower: multiway ANOVA (F-test / Means, ANOVA-fixed effects,special,main,interaction)
- Determine sample size for
reference example,
remember the between group variance ?- between group variance 1, within 16, sample size 128 (numerator df = 2-1)
- 2 x 2 with 0-2 → η2 as expected = .0588
- Get η2 for treatment effect but no type effect ? recognize f ?
- 0-2-4 for both types → f = .4082 of the omnibus F-test (compare all groups)
- Specify such that types differ, not treatment → f and sample size ?
- 0-0-0 versus 2-2-2 → f = .25 of t-test (compare two groups)
- Specify such that treatment effect only for one type → f and sample size ?
- 0-2-4 versus 0-0-0 → f = .2041, .25 and .2041
- detect interaction (num df = 2) = 235 total (40 per combination)
- detect only treatment effect (num df = 2) = 235 total (79 each group, 79/2 per combination)
- detect only type effect (num df = 1) = 128 total (64 each group, 64/3 per combination)
- detect both both main effects = 40 each combination ~ max(79/2,64/3)
- 0-2-4 versus 0-0-0 → f = .2041, .25 and .2041
- Specify effect for both treatment and type, without interaction → f and sample size ?
- 0-2-4 versus 2-4-6 → f = .4082, .25 and 0, sample size = 21 per combination
Repeated measures
If repeated measures → account for correlations within
Possible to focus on:
- within: similar to dependent t-test for multiple measurements
- between: group comparison, each based on multiple measurements
- interaction: difference between changes over measurements (within)
Correlation within unit (eg., within subject)
- informative within unit (like paired t-test)
- redundancy on information between units (observations less informative)
Beware: effect size could include or exclude correlation
GPower: repeated measures (F-test / Means, repeated measures...)
- correlation not yet included → Options: 'as in GPower 3.0'
- correlation already included → Options: 'as in SPSS'
- suggested youtube: https://www.youtube.com/watch?v=CEQUNYg80Y0
Repeated measures within
GPower: repeated measures (F-test / Means, repeated measures within factors)
Use effect size f = .25 (1/16 explained versus unexplained)
- mimic dependent t-test, correlation .5 !
- mimic independent t-test, but only use 1 group !
- double number of groups to 2, or 4 (cor = .5), what changes ?
- double number of measurements to 4 (cor = .5), impact ?
- compare impact double number of measurements for correlations .5 with .25 ?
- GPower: repeated measures (F-test / Means, repeated measures within factors)
- Mimic dependent t-test, correlation .5 !
- only 1 group, 2 repeated measures, correlation .5 → 34 x 2 measurements
- Mimic independent t-test, but only use 1 group !
- only 1 group, 2 repeated measures, correlation 0 → 65 x 2 measurements
- Double number of groups to 2, or 4 (cor = .5), what changes ?
- number of groups not relevant for within group comparison
- but requires estimation, changed degrees of freedom
- Double number of measurements to 4 (cor = .5), impact ?
- sample size reduces from 34 to 24, but 34x2=68, 24*4=96
- With 4 measurements (double) take halve the correlation (0.25), impact ?
- sample size 35, nearly 34
- 2 repeated measurements with corr .5, about same sample size as 4 repeats with corr .25
Solution for repeated measures within
- GPower: repeated measures (F-test / Means, repeated measures within factors)
- Mimic dependent t-test, correlation .5 !
- only 1 group, 2 repeated measures, correlation .5 → 34 x 2 measurements
- Mimic independent t-test, but only use 1 group !
- only 1 group, 2 repeated measures, correlation 0 → 65 x 2 measurements
- Double number of groups to 2, or 4 (cor = .5), what changes ?
- number of groups not relevant for within group comparison
- but requires estimation, changed degrees of freedom
- Double number of measurements to 4 (cor = .5), impact ?
- sample size reduces from 34 to 24, but 34x2=68, 24*4=96
- With 4 measurements (double) take halve the correlation (0.25), impact ?
- sample size 35, nearly 34
- 2 repeated measurements with corr .5, about same sample size as 4 repeats with corr .25
Repeated measures between
GPower: repeated measures (F-test / Means, repeated measures between factors)
Use effect size f = .25 (1/16 explained versus unexplained)
- compare 2 groups, each 2 measurements...
impact on sample size when correlation 0, .25 and .5 ? - double number of groups to 2, or 4 (cor = .5), what changes ?
- double number of measurements to 4 (cor = .5), impact ?
- compare impact number of measurements for different correlations .5 with .25 ?
- mimic independent t-test ?
- compare 2 groups, each 2 measurements...
- GPower: repeated measures (F-test / Means, repeated measures between factors)
- Use effect size f = .25 (1/16 explained versus unexplained)
- Compare 2 groups, each 2 measurements... impact on sample size when correlation 0, .25 and .5 ?
- increase in correlations results in increase in sample size (redundancy)
- Double number of groups to 2, or 4 (cor = .5), what changes ?
- increase in number of groups, small increase (estimation required) IF same effect size f
- Double number of measurements to 4 (cor = .5), impact ?
- increase in number of measurements, increases total number, but reduces number of units
- Compare impact number of measurements for different correlations .5 with .25 ?
- increase stronger if correlations stronger
- Mimic independent t-test ?
- 128 units, if .99 correlation with fully redundant second set
- 132 units (66*2), if 0 correlation with need to estimate four group (2x2) averages and correlation
Solution for repeated measures between
- GPower: repeated measures (F-test / Means, repeated measures between factors)
- Use effect size f = .25 (1/16 explained versus unexplained)
- Compare 2 groups, each 2 measurements...
impact on sample size when correlation 0, .25 and .5 ?- increase in correlations results in increase in sample size (redundancy)
- Double number of groups to 2, or 4 (cor = .5), what changes ?
- increase in number of groups, small increase (estimation required) IF same effect size f
- Double number of measurements to 4 (cor = .5), impact ?
- increase in number of measurements, increases total number, but reduces number of units
- Compare impact number of measurements for different correlations .5 with .25 ?
- increase stronger if correlations stronger
- Mimic independent t-test ?
- 128 units, if .99 correlation with fully redundant second set
- 132 units (66*2), if 0 correlation with need to estimate four group (2x2) averages and correlation
Repeated measures interaction within x between
GPower: repeated measures (F-test / Means, repeated measures within-between factors)
Option: calculate effect sizes: http://apps.icds.be/effectSizes/
- for sd = 4, with group with average 0-2-4, and with non-responsive (all 0):
- compare effect sizes for interaction with correlation .5 and 0, conclude ?
- compare sample sizes for those 2 effect sizes with correlation .5 or 0 ?
- GPower: repeated measures (F-test / Means, repeated measures within-between factors)
- Option: calculate effect sizes: http://apps.icds.be/effectSizes/
- For sd = 4, with group with average 0-2-4, and with non-responsive (all 0):
- Compare effect sizes for interaction with correlation .5 and 0, conclude ?
- with 0 correlation → f for interaction = .25
- with .5 correlation → f = .3536
- Compare sample sizes for those 2 effect sizes with correlation .5 or 0 ?
- for f = .25, sample sizes are 54x2 (cor=0) and 28x2 (cor=.5)
- for f = .3535, sample sizes are 28x2 (cor=0) and 16x2 (cor=.5)
- either include .5 correlation to calculate effect size OR sample size
Solution for repeated measures interaction within x between
- GPower: repeated measures (F-test / Means, repeated measures within-between factors)
- Option: calculate effect sizes: http://apps.icds.be/effectSizes/
- For sd = 4, with group with average 0-2-4, and with non-responsive (all 0):
- Compare effect sizes for interaction with correlation .5 and 0, conclude ?
- with 0 correlation → f for interaction = .25
- with .5 correlation → f = .3536
- Compare sample sizes for those 2 effect sizes with correlation .5 or 0 ?
- for f = .25, sample sizes are 54x2 (cor=0) and 28x2 (cor=.5)
- for f = .3535, sample sizes are 28x2 (cor=0) and 16x2 (cor=.5)
- either include .5 correlation to calculate effect size OR sample size
Correlations
If comparing two independent correlations
Use Fisher Z transformations to normalize first
- z = .5 * log( 1+r1−r ) → q = z1-z2
GPower: z-tests / correlation & regressions: 2 indep. Pearson r's
- with correlation coefficients .7844 and .5, what are the effect & sample sizes ?
- with the same difference, but stronger correlations, eg., .9844 and .7, what changes ?
- with the same difference, but weaker correlations, eg., .1 and .3844, what changes ?
Note that dependent correlations are more difficult, see manual
- GPower: z-tests / correlation & regressions: 2 indep. Pearson r's
- With correlation coefficients .7844 and .5, what are the effect & sample sizes ?
- effect size q = 0.5074, sample size 64*2 = 128
- .5∗log((1+.7844)/(1−.7844))−.5∗log((1+.5)/(1−.5))
- notice: effect size q ≈ d, same sample size
- With the same difference, but stronger correlations, eg., .9844 and .7, what changes ?
- effect size q = 1.5556, sample size 10*2 = 20
- same difference but bigger effect (higher correlations more easy to differentiate)
- With the same difference, but weaker correlations, eg., .1 and .3844, what changes ?
- effect size q = 0.3048, sample size 172*2 = 344
- same difference, negative, and smaller effect (lower correlations more difficult to differentiate)
Solution for correlations
- GPower: z-tests / correlation & regressions: 2 indep. Pearson r's
- With correlation coefficients .7844 and .5, what are the effect & sample sizes ?
- effect size q = 0.5074, sample size 64*2 = 128
- .5∗log((1+.7844)/(1−.7844))−.5∗log((1+.5)/(1−.5))
- notice: effect size q ≈ d, same sample size
- With the same difference, but stronger correlations, eg., .9844 and .7, what changes ?
- effect size q = 1.5556, sample size 10*2 = 20
- same difference but bigger effect (higher correlations more easy to differentiate)
- With the same difference, but weaker correlations, eg., .1 and .3844, what changes ?
- effect size q = 0.3048, sample size 172*2 = 344
- same difference, negative, and smaller effect (lower correlations more difficult to differentiate)
Proportions
If comparing two independent proportions → bounded between 0 and 1
GPower: Fisher Exact Test (exact / proportions, difference 2 independent proportions)
Effect sizes in odds ratio, relative risk, difference proportion
- for odds ratio 3 and p2 = .50, what is p1 ? and for odds ratio 1/3 ?
- what is the sample size to detect a difference for both situations ?
- for odds ratio 3 and p2 = .75, determine p1 and sample size,
how does it compare with before ? - for odds ratio 1/3 and p2 = .25, determine p1 and sample size,
how does it compare with before ? - compare sample size for a .15 difference, at p1=.5 ?
- GPower: Fisher Exact Test (exact / proportions, difference 2 independent proportions)
- For odds ratio 3 and p2 = .50, what is p1 ? and for odds ratio 1/3 ?
- odds ratio 3 → with p2 = .5 or odds_2 = 1, odds_1 = 3 thus p1 = 3/(3+1) = .75
- What is the sample size to detect a difference for both situations ?
- 128, same for .5 versus .25 or .75 (unlike correlation)
- For odds ratio 3 and p2 = .75, determine p1 and sample size,
how does it compare with before ?- p1 to .9, difference of .15, sample size increases to 220
- For odds ratio 1/3 and p2 = .25, determine p1 and sample size,
how does it compare with before ?- p1 to .1, difference of .15, sample size increases to 220
- Compare sample size for a .15 difference, at p1=.5 ?
- sample size even higher, to 366, increase not because smaller difference
Solution for proportions
- GPower: Fisher Exact Test (exact / proportions, difference 2 independent proportions)
- For odds ratio 3 and p2 = .50, what is p1 ? and for odds ratio 1/3 ?
- odds ratio 3 → with p2 = .5 or odds_2 = 1, odds_1 = 3 thus p1 = 3/(3+1) = .75
- What is the sample size to detect a difference for both situations ?
- 128, same for .5 versus .25 or .75 (unlike correlation)
- For odds ratio 3 and p2 = .75, determine p1 and sample size, how does it compare with before ?
- p1 to .9, difference of .15, sample size increases to 220
- For odds ratio 1/3 and p2 = .25, determine p1 and sample size, how does it compare with before ?
- p1 to .1, difference of .15, sample size increases to 220
- Compare sample size for a .15 difference, at p1=.5 ?
- sample size even higher, to 366, increase not because smaller difference
Exercise proportions
- GPower: Fisher Exact Test (exact / proportions, difference 2 independent proportions)
For odds ratio = 2, with p2 reference probability .6
Plot power over proportions .5 to 1
Include 5 curves, sample sizes 328, 428, 528...
With type I error .05
Explain curve minimum, relation sample size ?
Repeat for one-tailed, difference ?
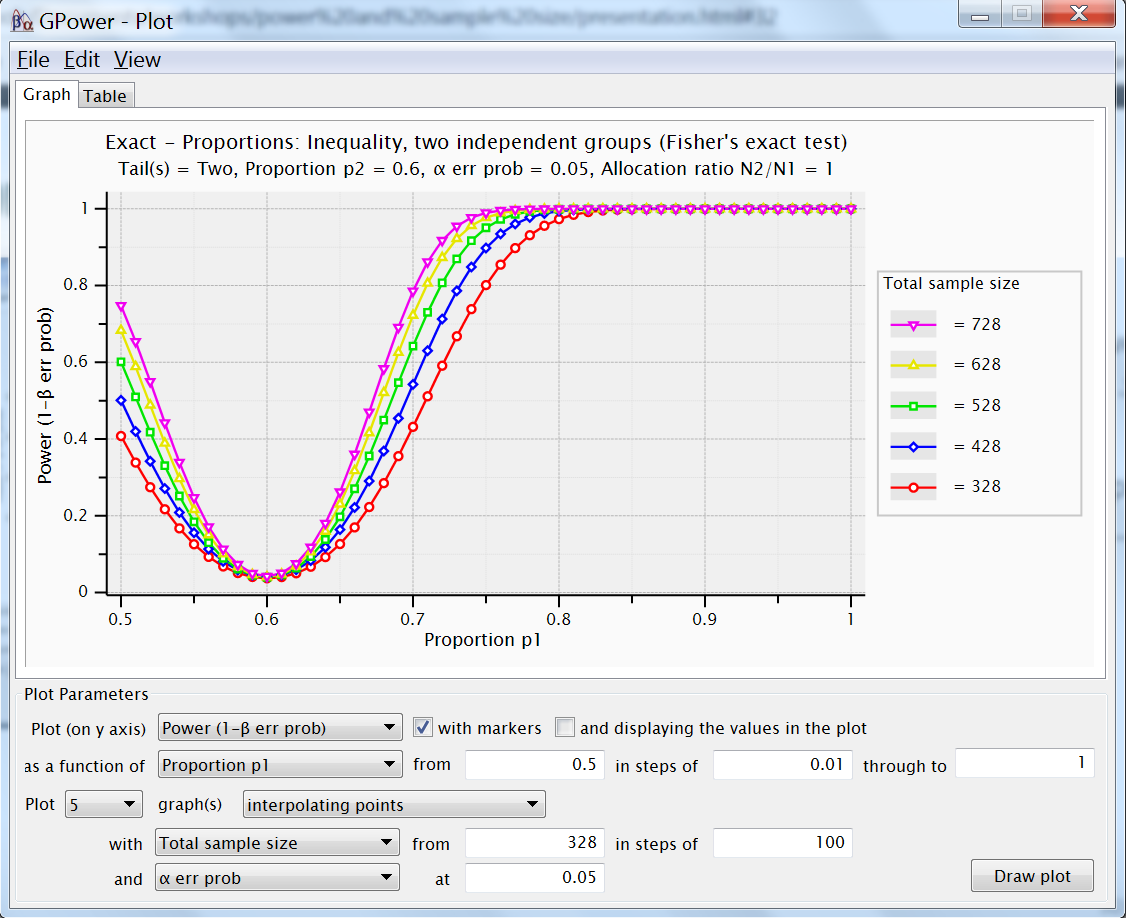
- For odds ratio = 2, with p2 reference probability .6
- Plot power over proportions .5 to 1
- Include 5 curves, sample sizes 328, 428, 528...
- With type I error .05
- Explain curve minimum, relation sample size ?
- power for proportion compared to reference .6
- minimum is type I error probability
- sample size determines impact
- Repeat for one-tailed, difference ?
- one-tailed, increases power (both sides !?)
Solution for proportions
- GPower: Fisher Exact Test (exact / proportions, difference 2 independent proportions)
- For odds ratio = 2, with p2 reference probability .6
- Plot power over proportions .5 to 1
- Include 5 curves, sample sizes 328, 428, 528...
- With type I error .05
- Explain curve minimum, relation sample size ?
- power for proportion compared to reference .6
- minimum is type I error probability
- sample size determines impact
- Repeat for one-tailed, difference ?
- one-tailed, increases power (both sides !?)

Dependent proportions
If comparing two dependent proportions → categorical shift
- if only two categories, McNemar test: compare p12 with p21
- information from changes only → discordant pairs
- effect size as odds ratio → ratio of discordance
- like other exact tests, choice assignment alpha
GPower: McNemar test (exact / proportions, difference 2 dependent proportions)
- assume odds ratio equal to 2, equal sized, type I and II errors .05 and .2, two-way !
- what is the sample size for .25 proportion discordant, .5, and 1 ?
- odds ratio 1 versus .5, (prop discordant = .25), what are p12 and p21 and sample sizes ?
- repeat for third alpha option, and consider total sample size, what happens ?
- GPower: McNemar test (exact / proportions, difference 2 dependent proportions)
- Assume odds ratio equal to 2, equal sized, type I and II errors .05 and .2, two-way !
- What is the sample size for .25 proportion discordant, .5, and 1 ?
- 288 (.25), 144 (.5), 73~144/2 (.99) → decrease in sample size with increased discordance
- Odds ratio .5 or 4, (prop discordant = .25), what are p12 and p21 and sample sizes ?
- same as 2 but reverse p12 and p21, with sample size 288
- with 4 as odds ratio, larger effect, requires smaller sample size, only 80
- odds ratio = p12 / p21
- Repeat for third alpha option, with odds ratio 4, what happens ?
- changed lower / upper critical N, lower sample size
- BUT, is because lower power, closer to requested .8
Solution for dependent proportions
- GPower: McNemar test (exact / proportions, difference 2 dependent proportions)
- Assume odds ratio equal to 2, equal sized, type I and II errors .05 and .2, two-way !
- What is the sample size for .25 proportion discordant, .5, and 1 ?
- 288 (.25), 144 (.5), 73~144/2 (.99) → decrease in sample size with increased discordance
- Odds ratio .5 or 4, (prop discordant = .25), what are p12 and p21 and sample sizes ?
- same as 2 but reverse p12 and p21, with sample size 288
- with 4 as odds ratio, larger effect, requires smaller sample size, only 80
- odds ratio = p12 / p21
- Repeat for third alpha option, with odds ratio 4, what happens ?
- changed lower / upper critical N, lower sample size
- BUT, is because lower power, closer to requested .8
Not included
Various statistical tests difficult to specify in GPower
- various statistics / parametervalues that are difficult to guestimate
- manual for more complex tests not always very elaborate
Various statistical tests not included in GPower
- eg., survival analysis
- many tools online, most dedicated to a particular model
Various statistical tests no formula to offer sample size
- simulation may be the only tool
- iterate many times: generate and analyze → proportion of rejections
- generate: simulated outcome ← model and uncertainties
- analyze: simulated outcome → model and parameter estimates + statistics
- simulation may be the only tool
Simulation example t-test
gr <- rep(c('T','C'),64)y <- ifelse(gr=='C',0,2)dta <- data.frame(y=y,X=gr)cutoff <- qt(.025,nrow(dta))my_sim_function <- function(){ dta$y <- dta$y+rnorm(length(dta$X),0,4) # generate (with sd=4) res <- t.test(data=dta,y~X) # analyze c(res$estimate %*% c(-1,1),res$statistic,res$p.value)}sims <- replicate(10000,my_sim_function()) # many iterationsdimnames(sims)[[1]] <- c('diff','t.stat','p.val')mean(sims['p.val',] < .05) # p-values 0.8029mean(sims['t.stat',] < cutoff) # t-statistics 0.8029mean(sims['diff',] > sd(sims['diff',])*cutoff*(-1)) # differences 0.8024Focus / simplify
Complex statistical models
- simulate BUT it requires programming and a thorough understanding of the model
- alternative: focus on essential elements → simplify the aim
Sample size calculations (design) for simpler research aim
- not necessarily equivalent to final statistical testing / estimation
- requires justification to convince yourself and/or reviewers
- successful already if simple aim is satisfied
- ignored part is not too costly
Example:
- statistics: group difference evolution 4 repeated measurements → mixed model
- focus: difference treatment and control last time point is essential → t-test
- argument: first 3 measurements low cost, interesting to see change
Conclusion
Sample size calculation is a design issue, not a statistical one
Building blocks: sample & effect sizes, type I & II errors
- establish any of these building blocks, conditional on the rest
Effect sizes express the amount of signal compared to the background noise
GPower deals with not too complex models
- more complex complex models imply more complex specification
- simplify using a focus, if justifiable → then GPower can get you a long way
Methodological and statistical support to help make a difference
SQUARE provides complementary support in methodology and statistics to our research community, for both individual researchers and research groups, in order to get the best out of them
SQUARE aims to address all questions related to quantitative research, and to further enhance the quality of both the research and how it is communicated
website: https://square.research.vub.be/ includes information on who we serve, and how
booking: https://square.research.vub.be/bookings for individual consultations